FRACCIONES
Son
una expresión particular de las divisiones que se utilizan para
representar las
partes que se toman de un objeto que ha sido dividido en partes
iguales.Por ejemplo, dividimos una pizza en 8 partes iguales y cogemos tres. Esto se representa por la siguiente fracción:
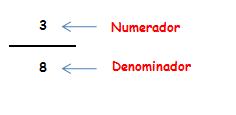
Los términos de la fracción se denominan: numerador y denominador.
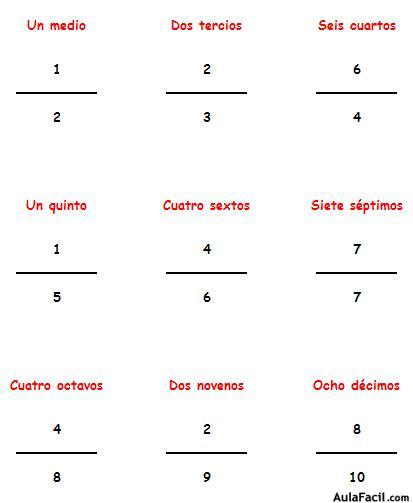
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
Las fracciones y sus partes
Veamos algunos ejemplos:
¿A cuantas unidades equivale una fracción? Para calcularlo se divide el numerador entre el denominador:
Por ejemplo:
Para ver a cuantas unidades equivale esta fracción dividimos: 2 : 8 = 0,25
Equivale a 0,25 unidades
Si una fracción tiene igual numerador y denominador representa la unidad.
Por ejemplo, divido una tarta en 4 partes y me tomo las cuatro partes:
Quiere decir que me he tomado la totalidad de la tarta (4 / 4), lo que equivale a la unidad (a la tarta). Si dividimos 4 : 4 = 1
1.- Fracciones equivalentes
Dos fracciones son equivalentes cuando equivalen a las mismas unidades.
Por ejemplo:
Estas dos fracciones son equivalente ya que equivalen a las mismas unidades:
4 : 8 = 0,5 unidades
1 : 2 = 0,5 unidades
¿Cómo sabemos cuando dos fracciones son equivalentes?
Para ello dividimos sus numeradores y sus denominadores, si guardan la misma proporción es que son equivalente:
Veamos un ejemplo:
Dividimos sus numeradores: 6 : 2 = 3
Dividimos sus denominadores: 9 : 3 = 3
Guardan la misma proporción (3) luego estas dos fracciones son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 6 : 9 = 0,66 unidades
La segunda fracción equivale a 2 : 3 = 0,66 unidades
Veamos ahora un ejemplo de dos fracciones que no son equivalentes:
Dividimos sus numeradores: 2 : 3 = 0,66
Dividimos sus denominadores: 4 : 9 = 0,44
No guardan la misma proporción luego estas dos fracciones no son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 2 : 4 = 0,50 unidades
La segunda fracción equivale a 3 : 9 = 0,33 unidades
Fracciones equivalentes
2.- Comparación de fracciones
¿Cómo puedo saber si una fracción es mayor o menor que otra?
Para ello vamos a distinguir:
Comparar fracciones con el mismo denominador
Comparar fracciones con distinto denominador
a) Comparar fracciones con el mismo denominador
Es mayor la fracción que tenga mayor el numerador.
Podemos comprobar que 2 / 4 = 0,5 mientras que 1 / 4 = 0,25, luego la primera fracción es mayor.
También podemos comprobar que 5 / 9 = 0,55 mientras que 3 / 9 = 0,33, luego la primera fracción es mayor.
b) Comparar fracciones con distinto denominador
En este caso puede ocurrir que tengan el mismo numerador o no.
b.1.- Si tienen el mismo numerador es mayor la que tenga menor denominador.
En este caso comprobamos que 8 / 3 = 2,66 mientras que 8 / 5 = 1,60, luego la primera fracción es mayor.
También podemos ver que 6 / 2 = 3,00 mientras que 6 / 4 = 1,50, luego la primera fracción es mayor.
b.2.- Si tienen distinto numerador entonces para poder comparalas hay que expresarlas con el mismo denominador:
Si los dos términos de una fracción se multiplican por el mismo número la fracción resultante es equivalente.
¿Y por qué número multiplicamos cada fracción? la primera fracción la multiplicamos por el denominador de la segunda, y la segunda por el denominador de la primera.
Veamos un ejemplo:
Para comparar estas dos fracciones, vamos a multiplicar los dos términos de la primera fracción por 2 (denominador de la segunda).
Podemos comprobar que al multiplicar numerador y denominador por el mismo número la fracción no cambia: 3 / 7 = 0,428 mientras que 6 / 14 = 0,428.
Y vamos a multiplicar los dos términos de la segunda fracción por 7 (denominador de la primera).
Ahora las dos fracciones ya tienen el mismo denominador, luego podemos compararlas:
Vemos que la segunda fracción es mayor que la primera porque su numerador es mayor.
Mayor y menor que
Comparación de números igual denominador
Comparación de números igual numerador
Cómo comparar fracciones y cómo usar el "mínimo común múltiplo" para eso... | ||
| Comparar fracciones Mínimo común múltiplo Herramienta para el mínimo común múltiplo Mínimo denominador común | ||
Cómo sumar, restar, multiplicar y dividir fracciones... | ||
 | ||
Cómo convertir fracciones en decimales y al revés... | ||
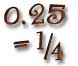 | Convertir decimales en fracciones Convertir fracciones en decimales | |
Cómo convertir fracciones en porcentajes y al revés... | ||
| Convertir porcentajes en fracciones Convertir fracciones en porcentajes | ||
Porcentajes (%)
Porcentaje quiere decir partes por 100
Cuando dices "por ciento" en realidad dices "por cada 100"
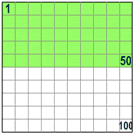 | Así que 50% quiere decir 50 por 100 (50% de la caja es verde) | 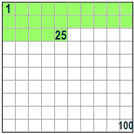 |
| Y 25% quiere decir 25 por 100 (25% de la caja es verde) |
Un porcentaje también se puede escribir como un decimal o una fracción
 |
| ||||||||||
Algunos ejemplos detallados
Calcula 25% de 80 | ||||||||||||||||||||||||||
| 25% = 25/100 | (25/100) × 80 = 20 | |||||||||||||||||||||||||
Así que 25% de 80 es 20
SI TE FIJAS, LO QUE HEMOS HECHO ES MULTIPLICAR 80 X 25 Y DIVIDIR EL RESULTADO POR 100. LA MULTIPLICACIÓN DA COMO RESULTADO 2000 Y AL DIVIDIR POR 100, NOS QUEDA JUSTAMENTE 20
| ||||||||||||||||||||||||||
Un Skateboard tiene una rebaja de 25%. El precio normal es 120 €. Calcula el nuevo precio | ||||||||||||||||||||||||||
Calcula 25% de 120 € | ||||||||||||||||||||||||||
| 25% = 25/100 | (25/100) × 120 = 30 | |||||||||||||||||||||||||
25% de 120 € es 30 € | ||||||||||||||||||||||||||
Así que la reducción es 30€ | ||||||||||||||||||||||||||
| Quita la reducción del precio original | 120 - 30 = 90 | |||||||||||||||||||||||||
El precio del Skateboard en rebajas es 90€
RECUERDA QUE OTRA MANERA DE RESOLVER ESTE TIPO DE PROBLEMAS ES DARTE CUENTA DE QUE SI TE REBAJAN UN 25 %, TE VAN A COBRAR EL 75 % ( EL RESTO DESDE 25 HASTA LLEGAR A 100 ). ASÍ, EL 75% DE 120 DA COMO RESULTADO 90.
| ||||||||||||||||||||||||||

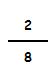
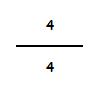

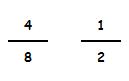
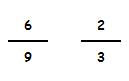
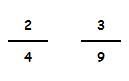


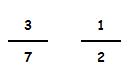
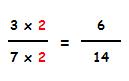
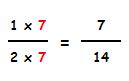
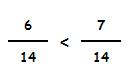

No hay comentarios:
Publicar un comentario